Search

» » Dislocation-induced stop-and-go kinetics of interfacial transformations - Nature.com

Dislocation-induced stop-and-go kinetics of interfacial transformations - Nature.com

paksijenong.blogspot.com

Abstract

Most engineering materials are based on multiphase microstructures produced either through the control of phase equilibria or by the fabrication of different materials as in thin-film processing. In both processes, the microstructure relaxes towards equilibrium by mismatch dislocations (or geometric misfit dislocations) across the heterophase interfaces1,2,3,4,5. Despite their ubiquitous presence, directly probing the dynamic action of mismatch dislocations has been unachievable owing to their buried nature. Here, using the interfacial transformation of copper oxide to copper as an example, we demonstrate the role of mismatch dislocations in modulating oxide-to-metal interfacial transformations in an intermittent manner, by which the lateral flow of interfacial ledges is pinned at the core of mismatch dislocations until the dislocation climbs to the new oxide/metal interface location. Together with atomistic calculations, we identify that the pinning effect is associated with the non-local transport of metal atoms to fill vacancies at the dislocation core. These results provide mechanistic insight into solid–solid interfacial transformations and have substantial implications for utilizing structural defects at buried interfaces to modulate mass transport and transformation kinetics.

This is a preview of subscription content

Access options

Buy article

Get time limited or full article access on ReadCube.

$32.00

Buy

All prices are NET prices.

Fig. 1: Formation of mismatch dislocations at the Cu2O/Cu interface.
Fig. 2: In situ TEM visualization of the stop-and-go ledge flow of the Cu2O → Cu interfacial transformations at 623 K and 5.3 Pa of H2 gas.
Fig. 3: In situ atomic-scale observations of the intermittent ledge flow regulated by mismatch dislocations during the Cu2O → Cu interfacial transformations at 623 K and 5.3 Pa of H2 gas flow.
Fig. 4: DFT modelling of the stop-and-go Cu2O → Cu interfacial transformations.

Data availability

All data generated or analysed during this study are included in the published article and its Supplementary Information files.

References

  1. Howe, J. M., Pond, R. C. & Hirth, J. P. The role of disconnections in phase transformations. Prog. Mater Sci. 54, 792–838 (2009).

    CAS  Article  Google Scholar 

  2. Ikuhara, Y. & Pirouz, P. High resolution transmission electron microscopy studies of metal/ceramics interfaces. Microsc. Res. Tech. 40, 206–241 (1998).

    CAS  Article  Google Scholar 

  3. Hirth, J. P. & Mitchell, T. E. The role of interface structure in oxidation reactions. Acta Mater. 56, 5701–5707 (2008).

    CAS  Article  ADS  Google Scholar 

  4. Ernst, F. Metal–oxide interfaces. Mat. Sci. Eng. R 14, 97–156 (1995).

    Article  Google Scholar 

  5. Du Plessis, J. & Van der Merwe, J. On pointed minima in the interfacial energy of bicrystal systems. Phil. Mag. 11, 43–51 (1965).

    Article  ADS  Google Scholar 

  6. Pieraggi, B., Rapp, R. A., van Loo, F. J. J. & Hirth, J. P. Interfacial dynamics in diffusion-driven phase transformations. Acta Metall. Mater. 38, 1781–1788 (1990).

    CAS  Article  Google Scholar 

  7. Zou, L. F. et al. Dislocation nucleation facilitated by atomic segregation. Nat. Mater. 17, 56–63 (2018).

    CAS  Article  ADS  Google Scholar 

  8. LaGrow, A. P., Ward, M. R., Lloyd, D. C., Gai, P. L. & Boyes, E. D. Visualizing the Cu/Cu2O interface transition in nanoparticles with environmental scanning transmission electron microscopy. J. Am. Chem. Soc. 139, 179–185 (2017).

    CAS  Article  Google Scholar 

  9. Zheng, H. M. et al. Multiferroic BaTiO3–CoFe2O4 nanostructures. Science 303, 661–663 (2004).

    CAS  Article  ADS  Google Scholar 

  10. Wang, C. M., Thevuthasan, S., Gao, F., McCready, D. E. & Chambers, S. A. The characteristics of interface misfit dislocations for epitaxial α-Fe2O3 on α-Al2O3(0001). Thin Solid Films 414, 31–38 (2002).

    CAS  Article  ADS  Google Scholar 

  11. Stach, E., Schwarz, K., Hull, R., Ross, F. & Tromp, R. New mechanism for dislocation blocking in strained layer epitaxial growth. Phys. Rev. Lett. 84, 947–950 (2000).

    CAS  Article  ADS  Google Scholar 

  12. Muller, D. A. et al. The electronic structure at the atomic scale of ultrathin gate oxides. Nature 399, 758–761 (1999).

    CAS  Article  ADS  Google Scholar 

  13. Hull, D. & Bacon, D. J. Introduction to Dislocations (Butterworth-Heinemann, 2001).

  14. Bollmann, W. Crystal Defects and Crystalline Interfaces (Springer-Verlag, 1970).

  15. Li, L. Z., Xie, L. & Pan, X. Q. Real-time studies of ferroelectric domain switching: a review. Rep. Prog. Phys. 82, 126502 (2019).

    CAS  Article  ADS  Google Scholar 

  16. Hirth, J. P., Pieraggi, B. & Rapp, R. A. The role of interface dislocations and ledges as sources/sinks for point defects in scaling reactions. Acta Metall. Mater. 43, 1065–1073 (1995).

    CAS  Article  Google Scholar 

  17. Hirth, J. Ledges and dislocations in phase transformations. Metall. Mater. Trans. A 25, 1885–1894 (1994).

    Article  Google Scholar 

  18. Sinclair, R. & Mohamed, H. A. Lattice imaging study of a martensite-austenite interface. Acta Metall. 26, 623–628 (1978).

    CAS  Article  Google Scholar 

  19. McGibbon, A. J., Pennycook, S. J. & Angelo, J. E. Direct observation of dislocation core structures in CdTe/GaAs (001). Science 269, 519–521 (1995).

    CAS  Article  ADS  Google Scholar 

  20. Ross, F. M. & Minor, A. M. in Springer Handbook of Microscopy (eds Hawkes, P. W. & Spence, J. C. H.) 101–187 (Springer, 2019).

  21. Stirman, J. N. & Crozier, P. A. Atomic-scale imaging of asymmetric Lomer dislocation cores at the Ge/Si(001) heterointerface. Appl. Phys. Lett. 84, 2530–2532 (2004).

    CAS  Article  ADS  Google Scholar 

  22. Gao, W. P., Sivaramakrishnan, S., Wen, J. G. & Zuo, J. M. Direct observation of interfacial Au atoms on TiO2 in three dimensions. Nano Lett. 15, 2548–2554 (2015).

    CAS  Article  ADS  Google Scholar 

  23. Minor, A. M. et al. A new view of the onset of plasticity during the nanoindentation of aluminium. Nat. Mater. 5, 697–702 (2006).

    CAS  Article  ADS  Google Scholar 

  24. Oh, S. H. et al. In situ observation of dislocation nucleation and escape in a submicrometre aluminium single crystal. Nat. Mater. 8, 95–100 (2009).

    CAS  Article  ADS  Google Scholar 

  25. Kacher, J., Eftink, B. P. & Robertson, I. M. Handbook of Mechanics of Materials 1–37 (Springer, 2018).

  26. Gutekunst, G., Mayer, J. & Rühle, M. The niobium/sapphire interface: structural studies by HREM. Scr. Metall. Mater. 31, 1097–1102 (1994).

    CAS  Article  Google Scholar 

  27. Sasaki, T. et al. Atomic and electronic structures of Ni/YSZ (111) interface. Mater. Trans. 45, 2137–2143 (2004).

    CAS  Article  Google Scholar 

  28. Mogck, S., Kooi, B. & De Hosson, J. T. M. Influence of metal–oxide interfaces on L12 ordering in Cu3Pd. Acta Mater. 52, 4651–4658 (2004).

    CAS  Article  ADS  Google Scholar 

  29. Sun, X. H. et al. Surface-reaction induced structural oscillations in the subsurface. Nat. Commun. 11, 305 (2020).

    CAS  Article  ADS  Google Scholar 

  30. Sun, X. H. et al. Atomic-scale mechanism of unidirectional oxide growth. Adv. Funct. Mater. 30, 1906504 (2020).

    CAS  Article  Google Scholar 

  31. Hÿtch, M. J., Snoeck, E. & Kilaas, R. Quantitative measurement of displacement and strain fields from HREM micrographs. Ultramicroscopy 74, 131–146 (1998).

    Article  Google Scholar 

  32. Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138 (1965).

    MathSciNet  Article  ADS  Google Scholar 

  33. Payne, M. C., Teter, M. P., Allan, D. C., Arias, T. & Joannopoulos, A. J. Iterative minimization techniques for ab initio total-energy calculations: molecular dynamics and conjugate gradients. Rev. Mod. Phys. 64, 1045–1097 (1992).

    CAS  Article  ADS  Google Scholar 

  34. Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).

    CAS  Article  ADS  Google Scholar 

  35. Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41, 7892–7895 (1990).

    CAS  Article  ADS  Google Scholar 

  36. Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).

    CAS  Article  ADS  Google Scholar 

  37. Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).

    CAS  Article  ADS  Google Scholar 

  38. Anisimov, V. I., Zaanen, J. & Andersen, O. K. Band theory and Mott insulators: Hubbard U instead of Stoner I. Phys. Rev. B 44, 943–954 (1991).

    CAS  Article  ADS  Google Scholar 

Download references

Acknowledgements

This work was supported by the US Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering under award number DE-SC0001135. This research used the resources of the Center for Functional Nanomaterials and the Scientific Data and Computing Center, a component of the Computational Science Initiative, at Brookhaven National Laboratory which is supported by the US Department of Energy, Office of Basic Energy Sciences, under contract number DE-SC0012704. This work also used the computational resources from the Extreme Science and Engineering Discovery Environment (XSEDE) through allocation TG-DMR110009, which is supported by National Science Foundation grant number OCI-1053575. This research used the resources of the Environmental TEM Catalysis Consortium (ECC) as well, which is supported by the University of Pittsburgh and Hitachi High Technologies.

Author information

Author notes

  1. These authors contributed equally: Xianhu Sun, Dongxiang Wu

Authors and Affiliations

  1. Department of Mechanical Engineering and Materials Science and Engineering Program, State University of New York at Binghamton, Binghamton, NY, USA

    Xianhu Sun, Dongxiang Wu, Lianfeng Zou, Xiaobo Chen & Guangwen Zhou

  2. Department of Chemical and Petroleum Engineering, University of Pittsburgh, Pittsburgh, PA, USA

    Stephen D. House, Meng Li & Judith C. Yang

  3. Center for Functional Nanomaterials, Brookhaven National Laboratory, Upton, NY, USA

    Dmitri N. Zakharov

Authors
  1. Xianhu Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Dongxiang Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Lianfeng Zou
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Stephen D. House
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Xiaobo Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  6. Meng Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  7. Dmitri N. Zakharov
    View author publications

    You can also search for this author in PubMed Google Scholar

  8. Judith C. Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  9. Guangwen Zhou
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

G.Z. conceived the experiments and supervised the project. X.S., L.Z., S.D.H. and X.C. conducted experiments. D.W. conducted DFT calculations. M.L. developed the codes for TEM image alignment. D.N.Z. and J.C.Y. contributed the experimental platform. X.S. and G.Z. analysed data and wrote the paper. All the authors commented on the manuscript.

Corresponding author

Correspondence to Guangwen Zhou.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature thanks Joshua Kacher and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. Peer reviewer reports are available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Extended data figures and tables

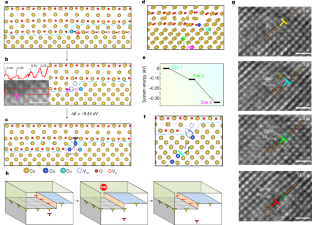
Extended Data Fig. 1 NEB calculations of energy barriers for vacancy-assisted diffusion of O atoms with the absence (upper panel) and presence (lower panel) of interstitial H in Cu2O.

a, Surface/subsurface: migration of an O atom in the second layer to a vacant lattice site in the topmost layer. b, Bulk: interlayer (1→0) and intralayer (2→0) O-vacancy exchanges. c, Cu2O/Cu interfacial ledge pinned at the mismatch dislocation core: migration of the O atom at the mismatch dislocation core to its adjacent, non-equivalent vacant lattice sites. d, Cu2O/Cu interface ledge away from the dislocation core by two Cu lattice spacings: migration of the O atom in front of the ledge to its adjacent, non-equivalent vacant lattice sites. e–h, Vacancy-assisted O diffusion along the same pathways as a–d with the presence of interstitial H in the Cu2O lattice.

Extended Data Fig. 2 DFT calculations of O-vacancy formation energies and Cu-vacancy exchange barriers.

Black arrows mark the O-vacancy formation (and the associated energy) at the interfacial ledge (2.1 eV) and terrace (2.6 eV), respectively, indicating that the Cu2O→Cu transformation occurs preferentially from the interfacial ledge, resulting in ledge flow. Blue arrows mark the interlayer Cu-vacancy exchange with and without the interfacial H, respectively, along two non-equivalent pathways in Cu2O. Green arrows mark atom-vacancy exchanges in the bulk of the Cu substrate. Cyan arrows mark the interfacial jumps of metallic Cu to the vacant site of the mismatch dislocation core in front of the interfacial ledge. Three non-equivalent types of atom-vacancy diffusion pathways are identified with the diffusion barriers in the range of 0.22 to 0.31 eV.

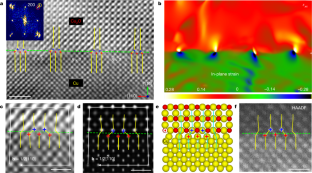
Extended Data Fig. 3 HRTEM and STEM-HAADF imaging of Cu vacancies in interfacial ledges.

a, b, HRTEM and HAADF images of the Cu2O(110)/Cu(110) interfaces showing the presence of a double-atomic-height interfacial ledge pinned at the mismatch dislocation core. c, d, HRTEM and HAADF images of the Cu2O(100)/Cu(100) interface showing a monoatomic interfacial ledge pinned at the mismatch dislocation. Shown on the right are the intensity profiles of the Cu2O/Cu interface region marked by the red dashed rectangle in a–d. The yellow arrows mark the interfacial ledges. The relatively dimmed image contrast of the atom column of the interfacial ledges compared to the neighbouring interfacial terrace Cu atom columns indicates the presence of Cu vacancies within the interfacial ledge. Scale bar: 0.5 nm.

Extended Data Fig. 4 HRTEM and HAADF simulations of interfacial ledges with different length ratios of the Cu and vacancy segments in the ledge.

a, b, Cu2O(110)/Cu(110) interface model with LCu/LV = 3 and 1 for the ledge atom columns marked by the cyan and green arrows, respectively, (LCu and LV stand for, respectively, the lengths of the Cu and vacancy segments in the ledge) before a and after b DFT relaxation. c, e, Simulated HRTEM and HAADF-STEM images based on the DFT relaxed interface structure in b. d, f, Intensity profiles drawn from the red rectangles in c and e, respectively. g, h, Cu2O(110)/Cu(110) interface model with LCu/LV = 1 and 1/3 in the two ledge atom columns marked by the green and yellow arrows, respectively, before g and after h DFT relaxation. i, k, Simulated HRTEM and HAADF-STEM images based on the DFT relaxed interface in h. j, l, Intensity profiles drawn from the purple rectangles in i and k, respectively, showing the decreased image intensity with increasing the length of the vacancy segment, consistent with the experimental HRTEM and HAADF images in Extended Data Fig. 3.

Extended Data Fig. 5 Energetically unfavourable events of interfacial ledge propagation and possible pathways for filling the vacancy column of the interfacial ledge.

a, b, Ledge flow without filling up the Cu-vacancy columns transforms the mismatch dislocation into an isolated edge dislocation in Cu. The mismatch dislocation (blue “T”) is buried by the newly formed Cu and becomes an isolated edge dislocation (red “T”), which will increase its energies due to the required presence of many broken bonds along the isolated dislocation line. By contrast, it is thermodynamically more favourable for the mismatch dislocations to climb to the new interface, by adsorbing extra Cu from the Cu substrate, to release some lattice mismatch strain upon the Cu2O→Cu interfacial transformation. c, An initially straight ledge stops at a mismatch dislocation core. d, e, A segment of Cu vacancies (marked in red colour) in front of the interfacial ledge is filled up and the segment then resumes its propagation to the next mismatch dislocation core (marked by the blue dashed lines). This is an unfavourable event because it will result in large geometric kinks with their side lengths of seven Cu lattice spacings for each propagation. Such an unsynchronized ledge flow leads to a highly kinked ledge with significantly increased ledge lengths and therefore is energetically unfavourable compared to the propagation of a straight ledge that happens only after all the Cu vacancies in front of the entire interfacial ledge are filled up. f–h, Two possible pathways of filling the vacancies in the interfacial ledge with Cu atoms supplied from the Cu bulk: f, g, randomly occupying the vacant sites, resulting in a high density of atomic kinks in the ledge; g, h, aggregation of Cu atoms into a one-dimensional (1D) segment of Cu, which subsequently grows along the ledge.

Extended Data Fig. 6 Evaluation of the system energy changes as a function of the distance of Cu vacancies from the Cu2O/Cu interface and of the aggregation of vacancies in the interfacial ledge.

a, The swap of one Cu vacancy in the dislocation core with a Cu atom that is away from the Cu2O/Cu interface by one, three and five atomic spacings in the Cu bulk, respectively. b, The swap of two Cu vacancies in the dislocation core with the Cu atoms that have increased distance from the Cu2O/Cu interface. c, Upper panel, Cu2O/Cu interfacial ledge consisting of isolated vacancies and Cu atoms; lower panel, Cu2O/Cu interfacial ledge consisting of 1D segments of aggregated Cu atoms and vacancies. The aggregation of vacancies (and Cu atoms) into 1D segments along the ledge lowers the system energy by 0.29 eV.

Extended Data Fig. 7 In situ HRTEM observations of the positive climb motion of edge dislocations in the bulk of the Cu substrate during the stop-and-go Cu2O→Cu transformation along the low-index Cu2O(110)/Cu(110) interface at 623 K and 5.3 Pa of H2 gas flow.

a, HRTEM micrograph showing the presence of edge dislocations (marked by yellow T) in the bulk of the Cu substrate. b, In situ HRTEM images (Supplementary Video 5) showing the glide and positive climb of an edge dislocation in the region marked with the blue dashed square in a. The edge dislocation has a projected Burgers vector of \(b=\frac{1}{2}[100]\) and is observed to glide (from yellow to cyan T positions) and climb (from cyan to red T positions) during the stop-and-go propagation of the interfacial ledges. Scale bar, 0.5 nm (a, b).

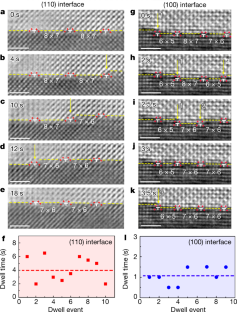
Extended Data Fig. 8 In situ HRTEM observations of the stop-and-go Cu2O→Cu transformation along a high-index Cu2O/Cu interface during the H2 exposure at 623 K and 0.021 Pa of H2 gas flow.

a–d, Time-sequence HRTEM micrographs (Supplementary Video 6) showing the presence of a high density of interfacial ledges that are constantly pinned at the mismatch dislocations during the Cu2O/Cu interface propagation toward the Cu2O side. The propagation of the interfacial ledges is accompanied by the glide and climb of the mismatch dislocation in front of the ledges. Meanwhile, an edge dislocation in the Cu bulk is observed to glide and climb deeper toward the Cu substrate during the Cu2O→Cu interfacial transformation. Scale bar, 2 nm.

Extended Data Fig. 9 (Left panel) In situ plan-view HRTEM imaging of the Cu2O(100)/Cu(100) interfacial transformation at 623 K and 5.3 Pa of H2 gas; (right panel) HRTEM simulation and intensity profile for the interfacial stop-and-go ledge flow along the e-beam direction.

a–d, Time-sequence HRTEM images (Supplementary Video 8) showing that the image contrast of the Cu2O(100)/Cu(100) interfacial layer marked with red, cyan, blue and green rectangles becomes progressively dimmed in an intermittent manner. e, Time-sequence intensity profiles along the interface layer marked in a–d, showing intermittent attenuation in the image intensity of atomic columns in the interface layer. Similar intensity profiles are grouped in the same colour. f, Time-sequence intensity profiles showing the constant image contrast of the pure Cu2O and Cu regions (marked by yellow and pink rectangles, respectively, in a–d). The intermittent attenuation of the image intensity within the Cu2O(100)/Cu(100) interface layer reveals that the Cu2O→Cu interfacial transformation occurs also via the stop-and-go ledge flow along the fore-and-aft direction that is parallel to the e-beam direction of the TEM imaging. g, h, Side- and front-views of the Cu2O(100)/Cu(100) interface model with the interfacial ledge pinning at the dislocation core. i–l, Simulated HRTEM images based on the front-view model (h), where the increased L1/L2 ratios correspond to the progressive Cu2O→Cu transformation within the Cu2O/Cu interface layer. The inset intensity profiles are extracted from the Cu2O/Cu interface layer marked by red dashed rectangles in the simulated HRTEM images. m, Intensity ratios of high/low peaks of the intensity profiles of the Cu2O/Cu interface of the simulated HRTEM images as a function of the L1/L2 ratio. n, Evolution of the intensity ratios of high/low peaks of the intensity profiles (e) of the Cu2O/Cu interface of the experimental HRTEM images as a function of the reaction time. Scale bar, 0.5 nm (a–d).

Extended Data Fig. 10 Pinning of interfacial ledges at the core of mismatch dislocations at a Cu2O/Cu interface formed from the oxidation of bulk Cu.

a, SEM image of a TEM lamella prepared by focus ion beam (FIB) milling of a bulk Cu sample oxidized at 423 K for 10 min in air under the atmospheric pressure. b, TEM image showing a high density of interfacial ledges that are pinned at the core of mismatch dislocations at the Cu2O/Cu interface. Insets: HRTEM images of the core region of the mismatch dislocations along with the pinned ledge. Scale bar, 5 \({\rm{\mu }}\)m (a), 2 nm (b).

Supplementary information

Rights and permissions

Reprints and Permissions

About this article

Verify currency and authenticity via CrossMark

Cite this article

Sun, X., Wu, D., Zou, L. et al. Dislocation-induced stop-and-go kinetics of interfacial transformations. Nature 607, 708–713 (2022). https://ift.tt/fxsZJvj

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://ift.tt/fxsZJvj

Comments

By submitting a comment you agree to abide by our Terms and Community Guidelines. If you find something abusive or that does not comply with our terms or guidelines please flag it as inappropriate.

Adblock test (Why?)



"Stop" - Google News
July 27, 2022 at 10:16PM
https://ift.tt/wTMV2fQ

Dislocation-induced stop-and-go kinetics of interfacial transformations - Nature.com
"Stop" - Google News
https://ift.tt/bISPTFV
https://ift.tt/IsO0kU2

Bagikan Berita Ini

0 Response to "Dislocation-induced stop-and-go kinetics of interfacial transformations - Nature.com"

Post a Comment

Subscribe to: Post Comments (Atom)
Powered by Blogger.